
数学の計算問題はできるけど、文章題が苦手…

勉強してはいるけど、何となく数学のテストの点・成績が上がらない…
そんな数学が苦手な中学生が、今すぐ、まずはじめにやるべきことを3つのまとめて解説します。
僕自身が中学の数学(より正確には小学生の算数)が苦手で、なかなかテストや成績で結果が出せませんでした。でも、これからお話しすることを意識して訓練した結果、「数学が得意・好き」とは言えないけど、しっかりと「テストで結果を出し・成績が上げる」状態にはなりました。具体的に言えば、定期テストで常に90点以上、成績は5段階中5という成果を出し続けることができるようになったのです。
ですから、現段階で数学が苦手という人でも、きちんとした考え方・やり方で訓練を積み重ねていけば大丈夫です。

※中学生の数学に関しては、具体的な単元ごとの問題解説動画を公開しています。主要な単元ごとの短めの解説動画ですので、苦手な単元のみをピンポイントで復習できると思います。解説動画内で使用している問題もPDFファイルで無料ダウンロードできます。ぜひ、学校の授業の復習や定期テスト・入試対策としてご活用ください。
数学が苦手な人が意識すべき3つのポイント【解説動画】
数学が苦手な人が「今すぐ」やるべき・意識して勉強するべき3つのポイントについてまとめた解説動画です。
記事の内容と合わせてぜひご覧ください。
数学が苦手な人がやるべき3つのポイント
数学が苦手な中学生が、今すぐ・まずやるべき3つのこととは、ズバリ…
②ノート・途中式の書き方を見直す
③「ことば」と「数式」の変換(文章題の立式)の方法を習得する
です。今回は、これら3つの加え、数学が苦手だという人に共通して見られる「割合」(分数・小数)の計算について「プラスアルファ」としてお話ししたいと思います。
計算問題は自信があるという人でも、分数や小数が含まれる計算問題になると、途端に正答率が下がる・計算ミスが増える場合があります。僕の経験上、これらのことは一部の人だけでなく、かなり多くの人が該当しています。
ぜひ、これを機に自分の学習を見直してみてください。
1.「計算問題」と「方程式」のちがい
「計算問題」と「方程式」を混同している生徒がたくさんいます。両者のちがいがはっきりと意識できていないからこその計算ミスは「あるある」と言っても良いほど、よく見る間違いです。
さて、では「計算問題」と「方程式」のちがいとは何でしょうか?
分かりやすいところでいえば、問題として与えられた式(与式)に「=」があるかないかという所です。「=」がない方が「計算問題」で、「=」がある方が「方程式」です。
さらに、両者の問題文がちがいます。普段あまり意識したことがないという人が多いかもしれませんね。ぜひ確認してみてください。「計算問題」は、多くの場合「次の計算をしなさい」という問題文です。一方、「方程式」は、「次の方程式を解きなさい」となっています。
これらの違いをふまえると、「計算問題」と「方程式」では、やることが全く違います。最終的な答え(ゴール)が全然ちがうのです。その点を意識しておかないと、やるべきことがきちんとできず、正確な解答に行きつきません。
では、両者のやるべきこと・目的(ゴール)の違いとは、一体何でしょうか?
【計算問題・方程式の目的(ゴール)】
「方程式」:(左辺=右辺を保ちながら)「Ⅹ=■■」の形にすること
両者のちがいをこのように捉えておくと良いでしょう。
すると、例えば、方程式では「分数の分母を約分して消すために、両辺に最小公倍数をかける」などの操作ができるということになります。が、計算問題では、同じような操作はできません。
計算問題と方程式を両方とも「計算問題」としてまとめて捉えている人は、両者の計算方法を混同してしまいがちです。数学が苦手だという人、いまお話しした点に心当たりがある人は、ぜひ「計算問題」と「方程式」のちがいと意識する所からはじめてみてください。
2.ノート・途中式の書き方
さて、では前項でお話しした「計算問題」と「方程式」のゴールのちがいを意識して、ゴールまでの道筋である「途中式」についてまとめておきましょう。
「計算問題」の途中式
まずは「計算問題」の途中式について確認していきます。

例えば、上のような計算問題を解く際に、どのように途中式を書くのが良いかと言えば・・・

②以降の式も左端に等号(=)を置いて途中式を書いていく
※等号(=)を縦一直線に並べて書く

「方程式」の途中式
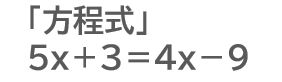
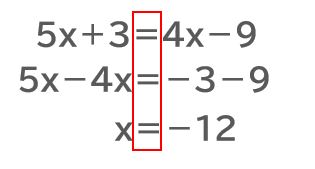

3.「ことば」と「数式」の変換(文章題)
ここでは、主に文章問題の立式(式をつくること)の基本的な考え方についてお話ししていきます。
例えば、次のような問題で式をつくる場合、どのように考えていけば良いでしょうか。実際に解きながら考えてみてください。

自然数を仮に□とすると、この問題の計算をそのまま書くと、次のようなわり算になります。
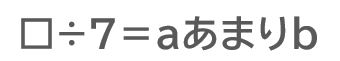
ですが、これでは「あまり」がことばですから、完全な数式に変換できていないことになります。このわり算の式を思い浮かべられる人は多いのですが、「あまり」という言葉を使わずに、完全な数式への変換がうまくできないという人が実際に多くいます。
では、そんな時、立式が上手くいかない時、どうすれば良いでしょうか?
おすすめの方法がこちら。

よく分からなくなってしまった時は、まず「自分が分かる計算式」に置きかえて考えてみるという方法を試してみてください。
今回の問題の場合は、例えば、「9÷2=4あまり1」という簡単なわり算の式を思い浮かべます。そして、「9」という元の数字を割る数「2」と商(わり算の答え)である「4」とあまり「1」を使って組み立てるには、どんな計算をするかを考えます。
すると、「9=2×4+1」(割る数×商+あまり)という式が導き出せるはずです。これは、いわゆる検算(たしかめ算)の式ですから、小学生でならっている内容です。
これがイメージできれば、あとは、それぞれの数字を今回の問題に置きかえ直して、式をつくっていけば良いというわけです。すると・・・

こういう形に式がつくれます。
それぞれの計算のかんたんな式は覚えていかなければいけません。が、文字式や方程式などの文章問題が苦手な人の中には、Xなどの文字が出てきて具体的なイメージがわかないという人が大勢います。そんな場合は、「自分が分かるかんたんな計算式」に置きかえて考えるという方法を取り入れてみると、わりとすっきり式をつくることができるのではないでしょうか。
さらに、もう一つだけ、文章問題の立式が苦手な人に、ちょっとした発想の転換ができることをお話ししておきます。文章問題が苦手な人の多くは、「文章問題」と聞いただけで「難しいもの」とイメージしてしまうようです。
ただし、中学生で学習する内容は、大きく分ければ「たし算」「ひき算」「かけ算」「わり算」の四則の計算しかないのです。意外と思われるかもしれませんが、中学生の数学の文章問題を学年問わず、分野問わず、いろいろならべて確認してみてください。どんなに複雑な式であっても、全体として「たし算」や「ひき算」をしていて、それぞれの項の中に「かけ算」や「わり算」があるという式が大半のはずです。
だから、文章問題の立式は、決して難しく考えず、「たし算」なのか「ひき算」なのか、それとも「かけ算」なのか「わり算」なのかを注意して考えていく作業なんだと思ってみましょう。そんな風に考えてみると、それほど難しいものではない印象になりませんか?
もちろん、印象の変化だけで確実に解けるようになるわけではありませんが、印象の変化はたいへん重要です。印象というのは、人に思考に大きな影響を与えるものですから、無意味に「難しい」と感じるのはできる限り避けた方が良いのです。
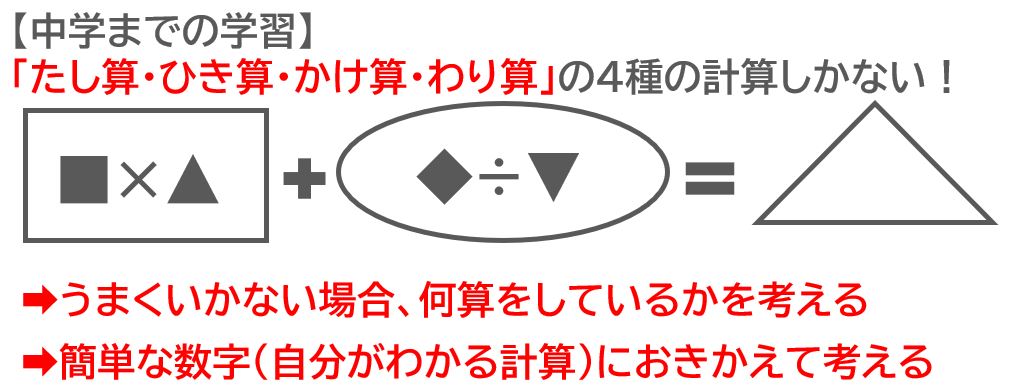
ぜひ、方程式の文章問題の式を大きな視点でながめてみてください(もちろん計算問題でもOKです)。上に示したように、大きく「たし算」「ひき算」でそれぞれの項で「かけ算」「わり算」をしている式がたくさん見つかるはずです。
そういう見方で式を見ることができるようになると、これまでよりもスッキリと式が立てられるようになると思います。
※より細かい説明は動画内でしています。この記事の冒頭部に貼り付けた動画をぜひご覧ください。
【プラスアルファ】割合(分数・小数)の計算
最後に「プラスアルファ」として、割合の計算についてお話ししておきます。
というのも、数学が苦手という人の多くが、割合をはじめとした分数や小数の計算が苦手である場合が非常に多いのです。僕自身も中学生のとき(正確には小学校高学年から)数学が苦手教科でしたが、やはり分数や小数の計算に難がありました。
特に、割合の考え方、計算方法は、単なるひとつの教科としての数学の学習に留まらず、大人になり、社会人になっても不可欠なものです。例えば、身近なお買い物にも密接に関わる「○○%OFF」とか消費税10%というのも、まさに割合です。こうした割合の計算や考え方が身に付いていないと、社会生活にも支障をきたす可能性があります。

ですから、まずは小学生の時に学習する「割合」「百分率」の内容から復習してみましょう。おそらく、多くの人は「60%」が「6割」と同じで、分数で表すと「100分の60」だということは分かるでしょう。苦手な人も基礎からやり直していけば、すぐに理解できるはずです。
問題は、そこからです。中学生になると「100分の60」のようなシンプルな分数で表現されたものだけではなく、様々な分数や小数が登場します。当然、文字式も頻繁に登場します。そうなると、途端にイメージができなくなる人が続出するようです(僕自身のそうでした(>_<))。
だからこそ、この基礎に立ち返って、基本的な「割合」の考え方・計算方法を徹底的に身につけるのです。そうすると、この記事でくり返しお話ししてきている「よく分からない時は自分の分かるかんたんな計算に置きかえて考える」際の武器として使えるからです。
方程式の文章問題の定番の「食塩水の濃度の問題」を解くには、「割合」の考え方が不可欠です。図形の線分比や面積比、体積比などの「比」の計算も「割合」のひとつです。数学が苦手な人はもちろん、数学で伸び悩んでいる人の原因は、もしかしたら「割合」の考え方・分数や小数、比の計算にあるのかもしれません。心当たりのある人は、ぜひ見直してみてください。
※中学生の数学に関しては、具体的な単元ごとの問題解説動画を公開しています。主要な単元ごとの短めの解説動画ですので、苦手な単元のみをピンポイントで復習できると思います。解説動画内で使用している問題もPDFファイルで無料ダウンロードできます。ぜひ、学校の授業の復習や定期テスト・入試対策としてご活用ください。
数学だけでなく、学習全般の「勉強方法」について関心のある方は、ぜひこちらの記事も合わせてご覧ください。
【中学生の勉強法】4ヶ月で全教科90点以上にした学習方法(超基礎編)






